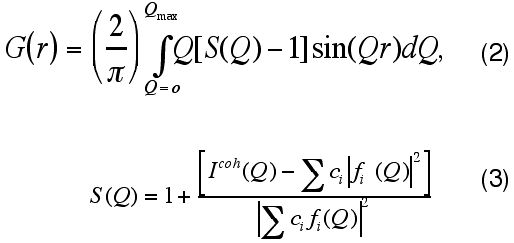
FUNDAMENTALS OF THE PDF TECHNIQUE
The PDF technique has the ability to see where Bragg diffraction (both single crystal and powder Rietvelt) cannot.
The atomic PDF, G(r), is defined as follows:
G(r) = 4p·r[r(r) - ro], (1)
where r (r) and r o are the local and average atomic number densities, respectively and r is the radial distance.
G(r) is a measure of the probability of finding an atom at a distance r from a reference atom and so describes the atomic arrangement, i.e. structure, of materials. It is the Fourier transform of the experimentally observable total structure factor, S(Q), i.e.
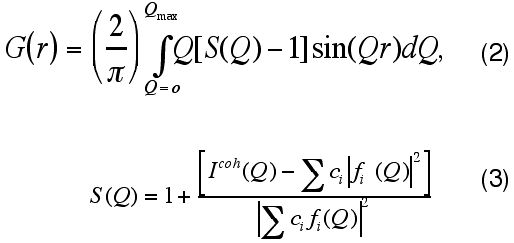
where Q is the magnitude of the wave vector (Q=4p sinq /l ). The structure factor S(Q) is related to the coherent part of the total diffracted intensity of the material.
Icoh.(Q) is the coherent scattering intensity per atom in electron units and ci and fi are the atomic concentration and X-ray scattering factor, respectively, for the atomic species of type i.
The following important details of the PDF technique are to be noted: G(r) is barely influenced by diffraction optics and experimental factors since these are accounted for in the step of extracting the coherent intensities from the raw diffraction data. This renders the PDF a structure-dependent quantity only. As Eq. 2 implies, the total, not only Bragg diffracted, intensities contribute to G(r). In this way both the long-range atomic structure, manifested in the sharp Bragg peaks, and the local structural imperfections, manifested in the diffuse components of the diffraction pattern, are reflected in the PDF. Also, by accessing high values of Q, experimental G(r)s with high real-space resolution can be obtained and, hence, quite fine structural features revealed.
Therefore, the PDF can serve as a basis for structure determination. Once the PDF is obtained an approach similar to Rietveld refinement is followed. A model atomic configuration is constructed and the respective PDF calculated and compared with the experimental one. Structural parameters in the model such as atomic positions, thermal factors and occupancies are then varied in such a way as to improve the agreement between the calculated and experimental PDFs. This is done with, or without, observing predefined constraints imposed by the symmetry of the space group of the crystal structure are tested. In this way, local distortions away from the average structure, or lower, unresolved, symmetries can be modeled.
The PDF is very sensitive to the coordination environment of atoms over short ( < 5 Å) and intermediate (5 Å - 20 Å) ranges. The approach has proven to be quite successful in determining the structure of various crystalline materials exhibiting different degrees of structural disorder.,, For example, it was possible to measure the local Jahn-Teller distortion around Mn ions in La1-xCaxMnO3.0 for which Rietveld refinement showed only the average structure that is an ideal MnO6 octahedron.
REFERENCES